One of the first few questions that I ask myself is what are technical indicators? Are they just a jumble of equations? In fact, most technical indicators are filters. A filter can be viewed as an equation that transforms a time series to another form, such as how moving averages are supposed to smooth a time series. The objective of a filter is to identify and extract certain features, such as the trend and cycles, from a time series. Filters are commonly used in most forms of analysis, such as in engineering, signals processing, image recognition, economics and finance. Hence, I cannot do justice without doing an article on filters. Even some of the more sophisticated models rely on effective filtering to work.
What a Filter does
In simple terms, a filter changes x to a different series y because you think that y makes it easier for you to analyze x, e.g. observe the trend in x. You can visualize this operation using the diagram below.

Filters can be classified into linear and non-linear types. There are other classifications such as infinite/finite impulse response and causal/non-causal filters which will be elaborated later. Whether an equation is linear or nonlinear is a mathematical construct. You can view the more rigorous explanations at the references below. Intuitively, a linear equation must obey the following rules
[Equations are typically represented by functions. For instance, f(x)=1 can refer to the equationx+2=1 or g(xy)=20 can refer to xy-9=20.]

Nonlinear equations do not obey the two rules above. The intuitive explanation of a nonlinear equation is one where changes in its input do not lead to a proportionate change in its output. An example of a nonlinear equation will be x2+x=2. A 50% change in x to 1.5 will cause x2+x=3.75, a 87.5% change.
Hence, it becomes obvious that x can be changed or mapped to y via functions that are either linear or nonlinear. The simple moving average, such as SMA3 below is an example of a linear filter, using n to denote the filter period or the number of historical periods this indicator averages.

The SMA3 of 1,2 and 3 is 2. If we increase 1, 2 and 3 respectively by 50% to 1.5, 3 and 4.5, SMA3 becomes 3, an equivalent increase of 50%. An example of a nonlinear function is a neural network whose explanation requires a separate post in itself.
Causal filters utilize the past and current values in mapping inputs to their outputs, like most technical indicators. Non-causal filters utilize both past and future values. An example will be a centered moving average.
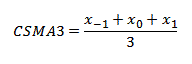
As future values are unobservable in real life, non-causal filters are more for analyzing and understanding current data than for predicting future values.
Types of Filter outputs
Filters are also classified based on their outputs into finite and infinite impulse response filters. An impulse response is a filter’s output to an unit impulse signal. Consider a “magical” option that costs $1 only on today and nothing on all other days, both future and current. Such a price sequence is called an unit impulse signal. Once the only non-zero input of 1 is entered into an infinite impulse response filter, this filter’s response or output will remain greater than 0 infinitely. An example of such a linear filter is the exponential moving average, EMA.
For a 3 period filter equivalent, or n=3, the EMA alpha = 2/(n+1) = 0.5

Suppose xo=1 and xi=0 for all other values of i. EMA will be 0 before x0. The EMA at x0 will be 0.5 x 0.50 x 1=0.5. For the next 10 days, x1 to x10 will be 0. However, EMA at x10 will be 0.5 x 0.510 x 1 = 0.000488. EMA after x0 will never be 0. The past filter outputs will always feedback to the current output. The simple moving average on the other hand is a finite impulse response filter. If filter period is 3, the SMA at x3 will be 0. Hence, the SMA will change abruptly when an older, but large observation is removed from the filter period, while the EMA phases out the older inputs gradually. Furthermore, the EMA is more responsive to the newer observations than the SMA. (See Chart below).

Conclusion
The key learning point of this article is to show that technical indicators are filters that extract features from a time series. It introduces different types of filters and illustrates how an unit impulse signal can be used to show the responsiveness and volatility of different technical studies.
However, a time series can also be represented as the sum of multiple oscillations with different frequencies and amplitudes. As the older values are never entirely excluded from the EMA, it is able to capture the effects of price patterns or cycle peaks and troughs that occur at higher frequencies or at intervals longer than the specified filter period. More will be elaborated on analyzing time series and filters as waves and signals in a separate article.
References
Gencay, Selcuk and Whitcher, 2002, An Introduction to Wavelets and Other Filtering Methods in Finance and Economics, Academic Press
An excellent book on wavelets analysis and filtering
A much more rigorous treatment of linear transformation
Like what you have just read? Digg it or Tip'd it.
The objective of Finance4Traders is to help traders get started by bringing them unbiased research and ideas. Since late 2005, I have been developing trading strategies on a personal basis. Not all of these models are suitable for me, but other investors or traders might find them useful. After all, people have different investment/trading goals and habits. Thus, Finance4Traders becomes a convenient platform to disseminate my work...(Read more about Finance4Traders)

0 comments:
Post a Comment