Excel VBA, Quantitative, Technical Analysis Research. Finance4Traders

Tuesday, June 30, 2009

Continued Fractions and the Modified Lentz's Method

This articles explains how to evaluate continued fractions and offers VBA code for Excel implementation

Continued fractions are of the form below

Continued fractions can be used to express certain numbers, such as π. They are also used in calculating bessel functions of fractional orders. A general method to evaluate continued functions is known as the modified Lentz's method.

The algorithm is consists of the following steps adapted from Press et. al.

f₀=b₀. If f₀=0 then let f₀=10^-30or an extremely small value ≈ 0.
C₀=f₀
D₀=0
For i=1 to a pre-determined number of iterations, e.g. 10000.
D_i=b_i+a_iD_i-1. If D_i=0, let D_i=10^-30or an extremely small value ≈ 0.
C_i=b_i+^a_i/_{C_i-1}. If C_i=0, let C_i=10^-30or an extremely small value ≈ 0.
D_i=¹/_{D_i}
Chg_i=C_iD_i
f_i=f_i-1Chg_i
Exit when |Chg_i-1| is smaller than a specified threshold.

These steps assume that you should stop when the change in f(x) becomes sufficiently small. By iterating the above twice, it becomes obvious how the algorithm works

The VBA implementation of the algorithm is as follows

Sub lentz()

'Declare your variables

Dim anow As Double, bnow As Double

Dim achange As Double, bchange As Double

Dim Cnow As Double, Dnow As Double

Dim fnow As Double, n As Long, Chgnow As Double

Dim small1 As Double, stop1 As Double

Dim answer As Range

'Set your variables

anow = 1

bnow = 2

achange = 1

bchange = 1

n = 9999

small1 = 10 ^ -30

stop1 = 10 ^ -15

Set answer = Range("B3")

'Start iterating

If bnow = 0 Then

fnow = small1

Else

fnow = bnow

End If

Cnow = fnow

Dnow = 0

For i = 1 To n

anow = anow + achange

bnow = bnow + bchange

Dnow = anow * Dnow + bnow

If Dnow = 0 Then Dnow = small1

Cnow = anow / Cnow + bnow

If Cnow = 0 Then Cnow = small1

Dnow = 1 / Dnow

Chgnow = Cnow * Dnow

fnow = fnow * Chgnow

If Abs(Chgnow - 1) <>

answer.Value = fnow

End

End If

Next i

answer.Value = fnow

End Sub

The code above is also adpated from Press et. al. However, it assumes that a_i and b_i will increase by 1 for each iteration.

References

Numerical Recipes The Art of Scientific Computing 3ed

William H. Press, Saul, A. Teukolsky, William T. Vetterling and Brian P. Flannery 2007

Cambridge University Press

Like what you have just read? Digg it or Tip'd it.

The objective of Finance4Traders is to help traders get started by bringing them unbiased research and ideas. Since late 2005, I have been developing trading strategies on a personal basis. Not all of these models are suitable for me, but other investors or traders might find them useful. After all, people have different investment/trading goals and habits. Thus, Finance4Traders becomes a convenient platform to disseminate my work...(Read more about Finance4Traders)

Please use this website in an appropriate and considerate manner. This means that you should cite Finance4Traders by at least providing a link back to this site if you happen to use any of our content. In addition, you are not permitted to make use of our content in an unlawful manner. You should also understand that our content is provided with no warranty and you should independently verify our content before relying on them. Do refer to the site content policy and privacy policy when visiting this site.

Time Series Analysis: Univariate and Multivariate Distributions

Introductory Concepts in Time Series Analysis

A time series refers to a set of data that is ordered by time. Price, volume and return data are three examples of time series. Time series can be discrete or continuous. In a discrete series, the time interval between each observation is an integer value. Continuous series are ordered by real numbers, the entire set of numbers that form the number line and need not necessarily refer to integers.

In the example above, we let x refer to the entire time series of stock prices and x can have many different values for its subscript i to refer to each individual observation in the time series. In this case, x₀ refers to the price today of $1.01. A single price is an observation. Strictly speaking, only x_i before x₀ are the realized observations, i.e. the historic prices.

Univariate and Multivariate Distributions and Time Series

When analyzing financial data, we often make comparisons involving more than one variable across time. When trading stocks, we may consider key information such as historical return, volume, dividend payout, profitability, sales growth etc. When a stock shows positive characteristics such as a low price-earnings ratio or strong historical price growth on high volume, we are more likely than not to expect positive future returns and buy into the stock.

Using terms borrowed from statistics and probability, we might be unknowningly making the assumption that the probability of a stock having a positive future return is greater than 50% given that its historical returns is more than 10% a year and its current profit growth is more than 20% annually. In mathematical notation, we may be assuming the following:

P[Future Return>0%|(Historical Return>10%, Current Profit Growth>20%)]>50%

If we are indeed making such assumptions, we must then believe that the future return of a stock given other information may take on multiple values with different probabilities. E.g.

P(Future Return = 5%|certain information=x) = 30%

P(Future Return = 10%|certain information=x)=15%

....

, where we let certain information and x be variables we use in our analysis such as profit growth =x% or volume =x lots traded etc.

The above are known as conditional probabilities. If we know the probability of observing certain information = x, P(certain information=x) = y%, we can convert these probabilities to joint probabilities using Bayes' rule.

P(A and B) = P (A|B) x P(B)

If we were to download 100 years of data for the Dow Jones Industrial Average and calculate the monthly return, we might observe the following univariate distribution.

On the other hand, we can calculate the returns in the past one month and in the next one month for every month of data we have to obtain the following possible distribution, which looks like a cone. Basically, it assigns a certain probability to every possible combination of current and future returns.

Thus it becomes apparent that by analyzing a set of variables to predict future return, we are inherently making probabilistic assumptions of future returns against available information. As such, we should shift our perspective of statistical distributions from a purely univariate case to a multivariate situation when studying related financial data.

The univarate case applies when the data we study has no relationship with each other. In the example above, the univariate distribution of monthly returns will be sufficient to tell us how much return we can expect in any month if we believe that historical returns do not affect future returns. If historical return share no relationship with future return, the probability of future return being a certain value x% will be the same regardless of historical return. If that is really the case, the multivariate distribution will be misleading. Hence, your chosen variables will determine your probability distribution which in turn affects your decision making process.

In reality, multivariate time series occur when we observe multiple related variables at the same point in time. An example will be price and volume. At time, t=0, you observe both the particular price and volume traded – 2 variables at the same time. If you assume that your series can go no more detailed than one day at a time, you can grudgingly argue that the open, high, low and closing prices are four variables observed at the same time. The crux of the issue is whether you correctly choose to include or exclude multiple variables in your analysis, to record an appropriate time series.

The distinction between these two time series is not trivial. Suppose you have been observing daily prices for a long time and you know that observing a price of $1.00 today gives you a 5% chance of observing a price of $1.20 tomorrow. Another person who observes both price and volume, might give only a 3% chance of observing a price of $1.20 tomorrow if today’s volume is 1000 shares traded.

Parametric Distributions

In practice, tabulating raw data might yield clumsy distributions that are not useful such as in the chart below.

In the case above, you will have dififculty inferring the probability of having a return of less than -10% or 14% or more than 15%. This happens when you have insufficient data or data that is not representative of what you believe to be the true distribution. To handle such situations, practitioners either apply smoothing techniques to their data or assume a parametic distribution such as the normal distribution or the student t distribution in their analysis.

Like what you have just read? Digg it or Tip'd it.

Site Updates

Hi (to whoever is reading this),

A big welcome for finding my site. This post is a running list of updates and work done on this site, inclusive of any on-going projects so that visitors including you can have a better understanding of the things I am doing.

11 July 09

Have not updated this journal for some time. Basically, I spent the last 2 weeks revamping the site layout. I tore the built-in template apart and redid everything from scratch. The benefit of literally reinventing the wheel is that I now know exactly how my template works and have done quite a few customisations to make it for pleasing to the eye.

I also wrote VBA functions and routines for each of the technical indicators featured here. Now all technical indicators here come with VBA code for your convenient implementation.

Two NEW articles have also been added for those who are more interesting in quant stuff. One of the articles is about multivariate distributions and why we should use them. Another is about analyzing technical indicators in the frequency domain.

26 June 09

Spent close to half a day trying to figure out a way to do web queries better in VBA. Turns out that it is much easier and simpler than I expected.

25 June 09

Did up an article on filtering. Interesting view on how you can test the how responsive or volatile some indicators are. Also did a less intensive article on recommended Excel programming practices. Hopefully someone finds it useful in increasing his productivity.

24 June 09.

I did some more posts on technical indicators and got to this indicator that went into signal processing. As stuffing everything about signals, filtering and hilbert transformation into a single post seems too ambitious, I opened up the quant section and did a few introductory stubs, while I tidy up my materials on filtering. The good thing about writing posts as you do your work is that it keeps you organized.

Sent a spreadsheet on VAR to a visitor earlier today.

23 June 09.

I have been writing about nothing but technical indicators for the last three days now. Why? I am currently on a mini-project to back test as many indicators as I can from a list of about 70 to 80 indicators. Once I am done with the back-tests, I will release them on this site.

Before I can do any actual backtesting, it came to me that I should spend time reading about technical indicators. Hence, I am posting them up as I read. The pace is slow because not all websites or books out there provide the exact formulas. Instead of explaining the steps involved in calculation, most websites give a brief explain what the indicator attempts to do and either continue with an example of using it to trade or recommend you to buy a trading tool or software. Over here, I do the reverse, I am brief about what the indicator does, but I go heavy into the formulas so that readers can implement these indicators themselves.

If you are serious about backtesting, you have know what drives a particular indicator. Hence, this is my addition to existing internet literature, a depository of 'how-to-calculate's - Anyone who wishes to know how an indicator is computed can come here. Some of them like the Fisher Transform or the Darvas Box are quite complex and a few websites do too brief a job explaining them.

The reason why I borther to do backtesting of technical indicators is because I intend to incorporate technical indicators in a genetic programming strategy that I will work on some time in the future.

22 June 09

I tried to do some marketing of my site on the 22nd by signing up to several forums and giving my 2 cents worth as a forum participant. Hey, I was not spamming ok! I diligently read the posts that other people write, respond to their comments with some of my own thoughts. Only if there are related topics will I send them to Finance4Traders. I only started one thread on possible unfavorable practices out there in the industry, after reading about all those angry customers who were disappointed with their brokers.

Yours sincerely,

Finance4Traders

Like what you have just read? Digg it or Tip'd it.

Signal Processing in Trading

Financial time series such as price data are in general digital signals. They can only take on a set range of values and can only be measured at discrete time intervals. Even tick data is digital. It is merely sampled at very small time intervals, i.e. the machine records the prevailing quote every millisecond and only shows you those that have changed.

Visit HERE for introductory information on signal processing and the terminology used here.

In fact any time series can be viewed as the summation of an infinite number of sine and cosine waves of varying amplitudes, phases and frequencies even if it is not periodic. A technique to break down a time series to its component sinusoidal waves is known as the Fourier transform. From this perspective, I assert that any particular financial time series may be characterised by waves of certain dominant frequencies. Understanding how a particular technical indicator and its parameters interact with these dominant frequencies can help the trader understand if his chosen indicator is extracting the information he or she wants.

Suppose the market goes through a mini cycle every 2 weeks, a 200 week moving average will never be able to identify the peaks and troughs of this mini cycle. The design of indicators may limit its ability to capture frequency dynamics within a certain bandwidth only. For example, a n period simple moving average will not be able to capture the cyclicity of a n period cycle as well as that of integer multiples of n period cycles.

An article HERE explains fitlers in trading and how they are classified within the time domain. The current article that you are reading elaborates on filters in the frequency domain. Filters and signals can be analyzed within the frequency or time/temproral domain.

In the frequency domain, filters are typically classified into low-band pass and high-band pass filters. A low-band pass filter tends to capture the low frequency dynamics of a signal, while a high-band pass filter captures the high frequency components of a signal. The following sections will help you understand what I mean.

Frequency Domain

The process of classifying filters in the frequency domain begins by feeding a signal x_t of a known frequency into the filter.

x_t=e^i2πft

Using the Euler's identity, e^i2πft actually equals cos(2πft)+isin(2πft) which produces signals like below, depending on the frequency of the signal. [This article here explains more about the role of the Euler's identity in signal processing.]

Using the 3 period simple moving average indicator in our previous article on filters and technical indicators, we obtain the following.

The function H(f) is the frequency response function or the transfer function of the signal and has the general form.

H(f) can be further broken into two parts - the gain function G(f) and phase angle θ as shown below.

In the case of the 3 period simple moving average, the gain function G(f) and phase angle of the filter θ are as follows,

The G(f) and θ that I work out above might not be accurate. While, I have retained the meaning behind these functions, I have not had them proof-read and they are for illustrative purpose only. If we fit H(f) and its component G(f) and θ back into the original filter

Recall that the original signal x_t=e^i2πft or x_t=cos(2πft)+isin(2πft). Hence, we now know that the three period simple moving average changes the the original signal by G(f) and introduces a phase shift of θf.

A high-band pass filter will have a G(f) whose magnitude is close to 1 at higher frequencies and a G(f) of magnitude approximately 0 at lower frequencies. The reverse applies to low-band pass filters. The magnitude of G(f) is calculated as √[(real coefficient)²+(imaginery coefficient)²]. The real and imaginery coefficients refer to the respective components of the G(f) function.

Intuitively, the product of 2 complex numbers (a+bi) and (c+di) is equal to (ac-bd)+(bc+ad)i. The magnitude of (ac-bd)+(bc+ad)i is equal to the product of the magnitudes of (a+bi) and (c+di). Recall that a time series can be viewed as a combination of signals with different frequencies. Hence, the outputs of a filter whose gain function G(f) has a magnitude of 1 at frequency f best reflect the component signal of that frequency. If θf is not zero, this means that the indicator shifts the phase of the input signal and and lags the input signal by θf/2π of a cycle.

The chart below is called a gain diagram and it shows the magnitude of the gain function of a 3 period simple moving average aginst the signal x_t=e^i2πft at varying frequencies. As can be observed, the gain function is approximately 0 at frequencies of 0.333 and 0.666, meaning that this indicator is unable to sufficiently reflect the dynamics of a 3 period and 6 period cycle.

Conclusion

While it seems like overkill to go through such complicated mathematics just to show that there is little utility in using a 3 period moving average in a 3 period cycle, the method described here can be applied to test other indicators for their ability to capture market cycles. An example is the exponential moving average whose gain diagram looks like the below. The exponential moving average due to its design is able to capture at least some of the dynamics of a wide range of frequencies and is less limited by its averaging period.

References

An Introduction to Wavelets and Other Filtering Methods in Finance and Economics by Ramazan Gencay, Faruk Selcuk and Brandon Whitcher

Like what you have just read? Digg it or Tip'd it.

Understanding Technical Indicators: Filters in Finance

One of the first few questions that I ask myself is what are technical indicators? Are they just a jumble of equations? In fact, most technical indicators are filters. A filter can be viewed as an equation that transforms a time series to another form, such as how moving averages are supposed to smooth a time series. The objective of a filter is to identify and extract certain features, such as the trend and cycles, from a time series. Filters are commonly used in most forms of analysis, such as in engineering, signals processing, image recognition, economics and finance. Hence, I cannot do justice without doing an article on filters. Even some of the more sophisticated models rely on effective filtering to work.

What a Filter does

In simple terms, a filter changes x to a different series y because you think that y makes it easier for you to analyze x, e.g. observe the trend in x. You can visualize this operation using the diagram below.

Filters can be classified into linear and non-linear types. There are other classifications such as infinite/finite impulse response and causal/non-causal filters which will be elaborated later. Whether an equation is linear or nonlinear is a mathematical construct. You can view the more rigorous explanations at the references below. Intuitively, a linear equation must obey the following rules

[Equations are typically represented by functions. For instance, f(x)=1 can refer to the equationx+2=1 or g(xy)=20 can refer to xy-9=20.]

Nonlinear equations do not obey the two rules above. The intuitive explanation of a nonlinear equation is one where changes in its input do not lead to a proportionate change in its output. An example of a nonlinear equation will be x²+x=2. A 50% change in x to 1.5 will cause x²+x=3.75, a 87.5% change.

Hence, it becomes obvious that x can be changed or mapped to y via functions that are either linear or nonlinear. The simple moving average, such as SMA3 below is an example of a linear filter, using n to denote the filter period or the number of historical periods this indicator averages.

The SMA3 of 1,2 and 3 is 2. If we increase 1, 2 and 3 respectively by 50% to 1.5, 3 and 4.5, SMA3 becomes 3, an equivalent increase of 50%. An example of a nonlinear function is a neural network whose explanation requires a separate post in itself.

Causal filters utilize the past and current values in mapping inputs to their outputs, like most technical indicators. Non-causal filters utilize both past and future values. An example will be a centered moving average.

As future values are unobservable in real life, non-causal filters are more for analyzing and understanding current data than for predicting future values.

Types of Filter outputs

Filters are also classified based on their outputs into finite and infinite impulse response filters. An impulse response is a filter’s output to an unit impulse signal. Consider a “magical” option that costs $1 only on today and nothing on all other days, both future and current. Such a price sequence is called an unit impulse signal. Once the only non-zero input of 1 is entered into an infinite impulse response filter, this filter’s response or output will remain greater than 0 infinitely. An example of such a linear filter is the exponential moving average, EMA.

For a 3 period filter equivalent, or n=3, the EMA alpha = 2/(n+1) = 0.5

Suppose x_o=1 and x_i=0 for all other values of i. EMA will be 0 before x₀. The EMA at x₀ will be 0.5 x 0.50 x 1=0.5. For the next 10 days, x₁ to x₁₀ will be 0. However, EMA at x₁₀ will be 0.5 x 0.5¹⁰ x 1 = 0.000488. EMA after x₀ will never be 0. The past filter outputs will always feedback to the current output. The simple moving average on the other hand is a finite impulse response filter. If filter period is 3, the SMA at x₃ will be 0. Hence, the SMA will change abruptly when an older, but large observation is removed from the filter period, while the EMA phases out the older inputs gradually. Furthermore, the EMA is more responsive to the newer observations than the SMA. (See Chart below).

Conclusion

The key learning point of this article is to show that technical indicators are filters that extract features from a time series. It introduces different types of filters and illustrates how an unit impulse signal can be used to show the responsiveness and volatility of different technical studies.

However, a time series can also be represented as the sum of multiple oscillations with different frequencies and amplitudes. As the older values are never entirely excluded from the EMA, it is able to capture the effects of price patterns or cycle peaks and troughs that occur at higher frequencies or at intervals longer than the specified filter period. More will be elaborated on analyzing time series and filters as waves and signals in a separate article.

References

Gencay, Selcuk and Whitcher, 2002, An Introduction to Wavelets and Other Filtering Methods in Finance and Economics, Academic Press

An excellent book on wavelets analysis and filtering

Rowland, Todd and Weisstein, Eric W. "Linear Transformation." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/LinearTransformation.html

A much more rigorous treatment of linear transformation

Like what you have just read? Digg it or Tip'd it.

Quick Basic Info on Math and Physics

This post is where all basic information is stored so that you can easily understand what I am talking about.

Introduction to Signals

1. A signal is a sequence of numbers

2. A signal consists is measured along two dimensions – displacement and time.

3. An analogue signal is a continuous signal varying in continuous time. Its displacement (from 0) and time can take on real values*. At each infinitely small interval in time, there is a displacement that can take on a value of infinite number of decimal places. Chart 1 on the right is an example of an analogue signal. Sound is an example of an analogue signal.

4. A digital signal has discrete displacements at discrete time intervals. Its values are limited to a given set and are observed at fixed intervals in time.

5. A signal can be discrete in amplitude, but continuous in time, or continuous in amplitude but discrete in time.

References

Digital Signal Processing: DSP & Applications

by Day Stranneby, 2001

Introduction to Oscillations

1. A cycle is a complete oscillation about an equilibrium position, 0. In chart 1, the signal completes one cycle somewhere between time 5 and 6.

2. The period of an oscillator is the amount of time needed to complete one cycle.

3. The frequency of an oscillator is the number of complete cycles per time interval. It is the inverse of period or (1/period).

4. The amplitude of an oscillator is the maximum displacement about the equilibrium position, 0.

*Intuitively, real values or numbers are not discrete and can exist in infinitely small intervals.

Introduction to Complex Numbers

1. A complex number has the form x+yi, where x is the real coefficient and y is the imaginery coefficient of the complex number. i is defined as the square root of -1 or √-1. Thus all real numbers have an imaginery coefficient of 0.

2. Complex numbers were originally created to solve certain polynomial functions. Consider the equation x²+1=0, whose solution is √-1 - a complex number.

3. Complex numbers are always plotted on the complex plane or in an argand diagram with the y axis being the imaginary coefficient and the x axis being the real coefficient.

3. In signal processing, complex numbers allow signals to be represented in a coordinate system, where the signal at any one point in time is represented by a real and imaginery component. Such representation allows for easy manipulation of 'complex frequencies' as we shall see later.

Suppose you have a sine function as a signal, y=sin(2πft), where f is the frequency of your signal. You will observe the following signal if frequency = 1, or 1 cycle is completed within 1 time interval.

As the signal is repetitive, the same signal can be represented via the argand diagram below. The radius of the circle represents the signal amplitude, while the angle θ theta = 2πft.

4. Upon closer study of the diagram above, we will realize that the Euler's identity, eⁱθ=cosθ+isinθ, is another representation of complex numbers. Note that cosθ=sin(θ+π/2).

5. Suppose we have a complex frequency f=a+ib so that we have a signal represented by e^st.

e^st=e^(a+ib)t

=e^ate^ibt

=e^at[cos(bt)+isin(bt)]

We know from previously that cos(bt)+isin(bt) creates a signal of constant frequency on the real plane like for instance, either of the two signals below.

However, multiplying [cos(bt)+isin(bt)] by e^atcreates a signal with varying frequency over time depending on the value of a such as the example below.

References

Digital Signal Processing Fundamentals by Ashfaq A Khan

Like what you have just read? Digg it or Tip'd it.

Fisher Transform (VBA Code)

The code below provides a convenient sub routine to perform the Fisher transform. The FT_1 sub routine uses the high and low prices of your dataset as its inputs. You will also need to specify a number n representing the length of the normalising period in the transformation process. The sub routine produces 5 columns of outputs - the median price, normalised median price, smoothed normalised median price, Fisher transform and smoothed Fisher transform.

The exact steps of the Fisher transform and the meaning of the outputs can be obtained from here, where a more detailed explanation of the Fisher transform is provided. This article focuses on the VBA code for this indicator.

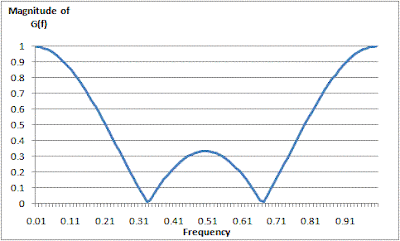
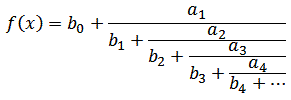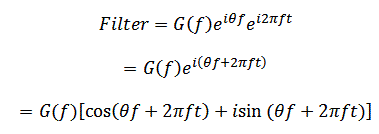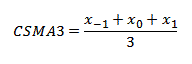Sub Runthis()

Dim high As Range, low As Range

Dim output As Range, n As Long

Set high = Range("C2:C11955")

Set low = Range("D2:D11955")

Set output = Range("H2:H11955")

n = 5 'number of historical periods to look at

'needed for certain indicators

FT_1 high, low, output, n

End Sub

Sub FT_1(high As Range, low As Range, output As Range, n As Long)

output(0, 1).Value = "Median Price"

high0 = high(1, 1).Address(False, False)

low0 = low(1, 1).Address(False, False)

output(1, 1).Value = "=(" & high0 & "+" & low0 & ")/2"

output(1, 1).Copy output

output(0, 2).Value = "Normalized Price"

rangen = Range(output(1, 1), output(n, 1)).Address(False, False)

TP = output(n, 1).Address(False, False)

output(n, 2).Value = "=(((" & TP & "-min(" & rangen & "))/(max(" & rangen & ")-min(" & rangen & ")))-0.5)*2"

output(n, 2).Copy output.Offset(0, 1)

output(0, 3).Value = "Smoothed Normalized Price"

SNPtoday = output(n + 1, 2).Address(False, False)

SNPyesterday = output(n, 3).Address(False, False)

output(n + 1, 3).Value = "=max(-0.9999,min(0.9999,(0.5*" & SNPtoday & "+0.5*" & SNPyesterday & ")))"

output(n + 1, 3).Copy output.Offset(0, 2)

SNPyesterday = output(n, 2).Address(False, False)

output(n + 1, 3).Value = "=max(-0.9999,min(0.9999,(0.5*" & SNPtoday & "+0.5*" & SNPyesterday & ")))"

output(0, 4).Value = "Fisher Transform"

SNP = output(n + 1, 3).Address(False, False)

output(n + 1, 4).Value = "=0.5*ln((1+" & SNP & ")/(1-" & SNP & "))"

output(n + 1, 4).Copy output.Offset(0, 3)

output(0, 5).Value = "Smoothed Fisher Transform"

FTtoday = output(n + 2, 4).Address(False, False)

FTyesterday = output(n + 1, 5).Address(False, False)

output(n + 2, 5).Value = "=0.5*" & FTtoday & "+0.5*" & FTyesterday

output(n + 2, 5).Copy output.Offset(0, 4)

FTyesterday = output(n + 1, 4).Address(False, False)

output(n + 2, 5).Value = "=0.5*" & FTtoday & "+0.5*" & FTyesterday

Range(output(1, 2), output(n - 1, 5)).Clear

Range(output(n, 3), output(n, 5)).Clear

output(n + 1, 5).Clear

End Sub

The code provided above is definitely not efficient and will be updated over time. If you have any suggestions, do drop a comment below.

Like what you have just read? Digg it or Tip'd it.

Average Directional Movement Rating

Average Directional Movement Rating ADR

Comes with formula, calculation steps and VBA code

Introduction

The average directional movement rating ADR is based on the average directional index ADX. You might want to read about the average directional index before proceeding further. The ADR is calculated as follows:

ADR=(current ADX + ADX k periods ago)/2

As such, ADR can be seen as an approximate of the average ADX over n periods. The crossover of ADR and ADX can be seen as a signal confirming the existing of the trend. ADX is a measure of the strength of a trend, not direction. In an up or down market, the ADR and ADX values are always positive. Therefore, these indicators should be used with other trend indicators to infer the direction of the market.

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate ADR. Method B is faster and more flexible.

Method A

To calculate average directional movement rating, ADR, you will need the ADX custom function in your code, which in turn needs the following custom functions from the respective pages

DM function from directional movement

WWMA function from Welles Wilder's moving average

TR function from average true range

DMX function from directional movement index

In addition, you will need to have calculated ADX using Method A based on the steps provided in the page on average directional index. Below is the code for the custom function ADR.

'Insert the following into the AddUDF sub which you can obtain from any of the 'other pages listed above.

Application.MacroOptions macro:="ADR", _

Description:="Returns Average Directional Movement Rating" & Chr(10) & Chr(10) & _

"Select current ADX and ADX n periods ago", _

Category:="Technical Indicators"

'Insert below into the module

Public Function ADR(ADX, ADXn)

ADR = (ADX + ADXn) / 2

End Function

Once done, you can calculate ADR by entering "=ADR([current ADX], [ADX k periods ago])" into any cell.

Method B

Method B is much more convenient, with the intermediate steps calculated for you. To run Method B, you have to copy the Runthis sub of Method B from the page on Accumulation/Distribution line. You will run the ADR_1 sub from the Runthis sub.

However, you will still need the DM_1, WWMA_1, ATR_1, DMI_1, DMX_1, ADX_1 subs of Method B from the directional movement, Welles Wilder's moving average, average true range, directional movement indicator, directional movement index and average directional index pages respectively.

'Copy the following line into the Runthis sub

'Just before the line End Sub

'Disable all other macros that Runthis will call e.g. CLV, ADL, by

'marking them out as comments with single quotes

ADR_1 high, low, close1, output, n, k

'Insert this as a new sub

Sub ADR_1(high As Range, low As Range, close1 As Range, output As Range, n As Long, k As Long)

ADX_1 high, low, close1, output, n

ADX0 = output(4 + k, 10).Address(False, False)

ADX1 = output(4, 10).Address(False, False)

output(0, 11).Value = "ADR"

output(4 + k, 11).Value = "=(" & ADX0 & "+" & ADX1 & ")/2"

output(4 + k, 11).Copy output.Offset(0, 10)

Range(output(1, 11), output(3 + k, 11)).Clear

End Sub

Other References

http://www.marketvolume.com/technicalanalysis/adxr.asp

Like what you have just read? Digg it or Tip'd it.

Weighted Moving Average

Weighted Moving Average WMA

Comes with formula, calculation steps and VBA code

The weighted moving average is calculated by giving each lagging price a smaller weight. The weight decreases at a constant rate from n to 0.

WMA = [n x Price_t + (n-1) x Price_t-1 + … + 2 x Price_t-n+2 + Price_t-n+1] / (n + (n-1) + …+ 2 + 1)

The divisor (n + (n-1) + …+ 2 + 1) can be calculated using the formula [n x (n+1)] / 2.

VBA Code

Two seperate methods are presented below.

Method A

To compute the weighted moving average of a series, enter into any cell "=WMA([n periods of your series])" after you have pasted the code below. The AddUDF sub routine adds your functions to a custom category called "Technical Indicators".

Sub AddUDF()

Application.MacroOptions macro:="WMA", _

Description:="Returns the Weighted Moving Average" & Chr(10) & Chr(10) & _

"Select n periods of prices", _

Category:="Technical Indicators"

End Sub

Public Function WMA(close_)

total1 = 0

n = WorksheetFunction.Count(close_)

divisor = (n * (n + 1)) / 2

For a = 1 To n

total1 = total1 + close_(a, 1) * a

Next a

WMA = total1 / divisor

End Function

Method B

In general, Method B is preferred over Method Afor large datasets. It is much more faster.

Sub Runthis()

Dim close1 As Range, output as Range, n As Long

Set close1 = Range("E2:E11955")

Set output = Range("H2:H11955")

n = 5 'number of historical periods to look at

'needed for certain indicators

WMA_1 close1, output, n

End Sub

Sub WMA_1(close1 As Range, output As Range, n As Long)

For a = 1 To n

output(a, 1).Value = a

Next a

numrange = Range(output(1, 1), output(n, 1)).Address

pricerange = Range(close1(1, 1), close1(n, 1)).Address(False, False)

output(n, 2).Value = "=sumproduct(" & numrange & "," & pricerange & ")/(" & n & "*(" & n & "+1)/2)"

output(n, 2).Copy output.Offset(0, 1)

Range(output(1, 2), output(n - 1, 2)).Clear

End Sub

Like what you have just read? Digg it or Tip'd it.

Directional Movement Index

Directional Movement Index DMX

Comes with formula, calculation steps and VBA code

Introduction

The directional movement index, DMX is derived from the positive and negative directional movement indicators, +DMI and -DMI. It is calculated as follows.

DMX = Absolute of [+DMI - (-DMI)] / [+DMI + (-DMI)]

The +DMI is the Welles Wilder's moving average of +DM over n days divided by the average true range for n days. -DMI is calculated in the same way. +DM refers to positive directional movement. Intuitively, it can be thought of as the change in the day's high. On the other hand, -DM or negative directional movement refers to the change in the day's low.

The directional movement index or DMX normalizes the absolute difference in DMI against the sum of +DMI and -DMI. It shows the strength in the current trend net of both upwards and downwards movement. If + DMI is similar in value to the -DMI, the value of DX will be small reflecting a weak trend. However, DX strictly tells nothing about the direction, only the strength of the trend because it is always an absolute value.

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate DMI. Method B is faster and more flexible.

Method A

To calculate +/-DMX, you need the following custom functions from the respective pages

DM function from directional movement

WWMA function from Welles Wilder's moving average

TR function from average true range

Calculate the following.

+DM and -DM, "=DM([current high], [current low], [previous high], [previous low])". Select the cell and the neigbouring cell right next to it, press F2 and Crtl+Shift+Enter. DM is an array function, returning both +DM and -DM
WWMA for +/- DM by entering in another cell "=WWMA([previous WWMA],[current +/-DM],[n])".
True range, "=TR([high],[low],[previous close])"
Average true range, "=WWMA([previous WWMA],[current TR],[n])"
+/-DMI=output from step 2 /output from step 4
DMX, "=DMX([+DMI],[-DMI])

'Paste this code into your ThisWorkBook code window in VBA. Right Click This WorkBook in Project Explorer and click View Code.

Private Sub Workbook_Open()

AddUDF

End Sub

'The rest belong to any module

Sub AddUDF()

'Tells Excel to includes these in list of functions, add descriptions to them and create a new category called Technical Indicators.

Application.MacroOptions macro:="DMX", _

Description:="Returns Directional Movement Index" & Chr(10) & Chr(10) & _

"Select positive and negative directional movement indicators", _

Category:="Technical Indicators"

End Sub

Public Function DMX(PosDMI, NegDMI)

DMX = Abs(PosDMI - NegDMI) / (PosDMI + NegDMI)

End Function

Method B

Method B offers the benefit of not having to the intermediate outputs, such as DMI yourself. It does everything for you. To run Method B, you have to copy the Runthis sub of Method B from the page on Accumulation/Distribution line. You will run the DMX_1 sub from the Runthis sub.

You will also need the DMI_1, DM_1, WWMA_1, ATR_1 subs of Method B from the directional movement indicator, directional movement, Welles Wilder's moving average and the average true range pages respectively.

'Copy the following line into the Runthis sub

'Just before the line End Sub

'Disable all other macros that Runthis will call e.g. CLV, ADL, by

'marking them out as comments with single quotes

DMX_1 high, low, close1, output, n

'Insert this as a new sub

Sub DMX_1(high As Range, low As Range, close1 As Range, output As Range, n As Long)

DMI_1 high, low, close1, output, n

output(0, 9).Value = "DMX"

PosDMI = output(3, 7).Address(False, False)

NegDMI = output(3, 8).Address(False, False)

output(3, 9).Value = "=abs(" & PosDMI & "-" & NegDMI & ")/(" & PosDMI & "+" & NegDMI & ")"

output(3, 9).Copy output.Offset(0, 8)

Range(output(1, 9), output(2, 9)).Clear

End Sub

Other References

http://fxtrade.oanda.com/learn/graphs/indicators/adx.shtml

Like what you have just read? Digg it or Tip'd it.

Directional Movement Indicator

Directional Movement Indicator DMI

Comes with formula, calculation steps and VBA code

Introduction

The directional movement indicator DMI is the directional movement smoothed by the Welles Wilder's moving average normalized by the average true range. Like directional movement, the DMI is made of two studies - Positive DMI and Negative DMI or +DMI and -DMI respectively. Both +DMI and -DMI are behave like indices and are positive numbers. The +DMI and -DMI measures the strength of the up and the down trends respectively.

+DMI=WWMA(+DM,n) / ATR(n)

-DMI=WWMA(-DM,n) / ATR(n)

, where WWMA(DM,n) refers to a n period Welles Wilder's moving average of the DM and ATR(n) refers to a n day average true range.

Smoothing the DM and dividing the result by average range allows the DMI to be compared across different trading ranges and hence, across time. On the other hand, an upward sloping WWMA of the DMI alone may be inflated by a spike in trading ranges.

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate DMI. Method B is faster and more flexible.

Method A

To calculate +/-DMI, insert into a module the DM function from the page on directional movement, WWMA function from the page on Welles Wilder's moving average and TR function from the page on average true range.

Calculate +DM and -DM, by entering into any cell "=DM([current high], [current low], [previous high], [previous low])". Select the cell and the neigbouring cell right next to it, press F2 and Crtl+Shift+Enter.
Calculate WWMA for +/- DM by entering in another cell "=WWMA([previous WWMA],[current +/-DM],[n])".
Calculate true range, "=TR([high],[low],[previous close])".
Calculate average true range "=WWMA([previous WWMA],[current TR],[n])".
+/-DMI = ouput from step 2 / output from step 4

Method B
Method B is more convenient as it does not require you to remember the computation steps. To run Method B, you have to copy the Runthis sub of Method B from the page on Accumulation/Distribution line. You will run the DMI_1 sub from the Runthis sub.

You will need the DM_1, WWMA_1, ATR_1 subs of Method B from the directional movement, Welles Wilder's moving average and the average true range pages respectively.

'Copy the following line into the Runthis sub
'Just before the line End Sub
'Disable all other macros that Runthis will call e.g. CLV, ADL, by
'marking them out as comments with single quotes
DMI_1 high, low, close1, output, n

'Insert this as a new sub
Sub DMI_1(high As Range, low As Range, close1 As Range, output As Range, n As Long)
DM_1 high, low, output
WWMA_1 output, output.Offset(0, 2), n
WWMA_1 output.Offset(0, 1), output.Offset(0, 3), n
Range(output(2, 3), output(2, 4)).Copy output(3, 3)
Range(output(2, 3), output(2, 4)).Clear
ATR_1 high, low, close1, output.Offset(0, 4), n
output0 = output(3, 3).Address(False, False)
output1 = output(3, 4).Address(False, False)
output2 = output(3, 6).Address(False, False)
output(0, 7).Value = "Positive DMI"
output(3, 7).Value = "=" & output0 & "/" & output2
output(3, 7).Copy output.Offset(0, 6)
output(0, 8).Value = "Negative DMI"
output(3, 8).Value = "=" & output1 & "/" & output2
output(3, 8).Copy output.Offset(0, 7)
Range(output(1, 7), output(2, 8)).Clear
End Sub

Other References

http://fxtrade.oanda.com/learn/graphs/indicators/adx.shtml

Like what you have just read? Digg it or Tip'd it.

Monday, June 29, 2009

Average True Range

Average True Range ATR

Comes with formula, calculation steps and VBA Code

The average true range is the Welles Wilder's moving average, WWMA of the true range, TR of a period. It is calculated as follows.

ATR=WWMA of TR

TR_t=max of (High_t,Close_t-1) - min of (Low_t,Close_t-1)

ATR=(TR_t+(n-1) x (WWMA of TR)_t-1) / n

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate APZ. Method B is faster and more flexible.

Method A

The average true range can be calculated by first computing the true range, before applying the WWMA function to it. The WWMA function can be obtained from here. The function for true range is as follows

'Paste this code into your ThisWorkBook code window in VBA. Right Click This WorkBook in Project Explorer and click View Code.

Private Sub Workbook_Open()

AddUDF

End Sub

'The rest belong to any module

Sub AddUDF()

'Tells Excel to includes these in list of functions, add descriptions to them and create a new category called Technical Indicators.

Application.MacroOptions macro:="TR", _

Description:="Returns True Range" & Chr(10) & Chr(10) & _

"Select current high, current low, last period's close.", _

Category:="Technical Indicators"

End Sub

Public Function TR(high, low, CloseYesterday)

TR = WorksheetFunction.Max(high, CloseYesterday) - WorksheetFunction.Min(low, CloseYesterday)

End Function

To compute true range, you just have to enter into any cell, "=TR([high],[low],[previous close])". The ATR can be computed by entering, "=WWMA([previous WWMA],[current TR],[n])".

Method B

Method B offers the benefit of not having to calculate true range yourself. It does everything for you. To run Method B, you have to copy the Runthis sub of Method B from the page on Accumulation/Distribution line and the WWMA_1 sub from the page on Welles Wilder's moving average. You will run the ATR sub from the Runthis sub.

'Copy the following line into the Runthis sub
'Just before the line End Sub
'Disable all other macros that Runthis will call e.g. CLV, ADL, by
'marking them out as comments with single quotes
ATR high, low, close1, output, n

Sub ATR(high As Range, low As Range, close1 As Range, output As Range, n As Long)
'Get true range
output(0, 1).Value = "True Range"
high0 = high(2, 1).Address(False, False)
low0 = low(2, 1).Address(False, False)
close0 = close1(1, 1).Address(False, False)
output(2, 1).Value = "=max(" & high0 & "," & close0 & ")-min(" & low0 & "," & close0 & ")"
output(2, 1).Copy output
output(1, 1).Clear
'Get ATR
output0 = output(4, 1).Address(False, False)
output1 = output(3, 2).Address(False, False)
output(4, 2).Value = "=(" & output0 & "+(" & n & "-1)*" & output1 & ")/" & n
output(4, 2).Copy output.Offset(0, 1)
Range(output(1, 2), output(2, 2)).Clear
output0 = output(3, 1).Address(False, False)
output1 = output(2, 1).Address(False, False)
output(3, 2).Value = "=(" & output0 & "+(" & n & "-1)*" & output1 & ")/" & n
End Sub

Other References

http://fxtrade.oanda.com/learn/graphs/indicators/adx.shtml#atr

Like what you have just read? Digg it or Tip'd it.

Average Directional Index

Average Directional Index ADX

Comes with formula, calculation steps and VBA code

Introduction

The average directional index, ADX is a relatively complex indicator involving a total of five other technical studies. They are Welles Wilder's moving average, average true range, directional movement, directional movement indicator and directional movement index. The ADX is a measure of trend strength, but not a measure of direction. You might want to visit the pages above before reading further.

The calculation of the ADX invovles four major steps.

Calculate the directional movement of each period based on the period high and low.
Smooth the directional movement using the Welles Wilder's moving average and divide the result by the average true range for the last n days to obtain the directional movement indicator.
Compute the directional movement index from the directional movement indicator to determine the strength of prevailing trend.
Smooth the directional movement index using the Welles Wilder's moving average to obtain the average directional index.

Thus, the ADX is a smoothed view of trend strength. The ADX does not measure market direction because the directional movement index is always a positive value. Its formula is as follows:

ADX=WWMA of DMX over k periods

VBA Code
Method A uses functions, while Method B uses sub procedures to calculate DMI. Method B is faster and more flexible.

Method A
To calculate average directional index, ADX, you need the following custom functions from the respective pages

DM function from directional movement
WWMA function from Welles Wilder's moving average
TR function from average true range
DMX function from directional movement index

Calculate the following.
+DM and -DM, "=DM([current high], [current low], [previous high], [previous low])". Select the cell and the neigbouring cell right next to it, press F2 and Crtl+Shift+Enter. DM is an array function, returning both +DM and -DM
WWMA for +/- DM by entering in another cell "=WWMA([previous WWMA],[current +/-DM],[n])".
True range, "=TR([high],[low],[previous close])"
Average true range, "=WWMA([previous WWMA],[current TR],[n])"
+/-DMI=output from step 2 /output from step 4
DMX, "=DMX([+DMI],[-DMI])
ADX, "=WWMA([previous ADX], [current DMX], [n])"
As can be seen, the calculation of the ADX is actually a WWMA function of DMX. I try to avoid writing custom functions that only run another custom function because it is repetitive. The function of ADX if I were to write one, will look like this

Public Function ADX(ADXPrevious, DMX, n)
ADX=WWMA(ADXPrevious,DMX,n)
End Function

Sub AddUDF()
Application.MacroOptions macro:="ADX", _
Description:="Returns Average Directional Movement Index" & Chr(10) & Chr(10) & _
"Select previous period's ADX, current DMX and n", _
Category:="Technical Indicators"
End Sub

The ADX function above merely passes the same inputs to the WWMA function.

Method B
Method B is much more convenient because it calculates the intermediate outputs for you. To run Method B, you have to copy the Runthis sub of Method B from the page on Accumulation/Distribution line. You will run the ADX_1 sub from the Runthis sub.

You will need the DM_1, WWMA_1, ATR_1, DMI_1, DMX_1 subs of Method B from the directional movement, Welles Wilder's moving average, the average true range, directional movement indicator, directional movement index pages respectively.

'Copy the following line into the Runthis sub
'Just before the line End Sub
'Disable all other macros that Runthis will call e.g. CLV, ADL, by
'marking them out as comments with single quotes
ADX_1 high, low, close1, output, n

'Insert this as a new sub
Sub ADX_1(high As Range, low As Range, close1 As Range, output As Range, n As Long)
DMX_1 high, low, close1, output, n
WWMA_1 output.Offset(0, 8), output.Offset(0, 9), n
output(0, 10).Value = "ADX"
output(2, 10).Copy output(4, 10)
Range(output(2, 10), output(3, 10)).Clear
End Sub

ADX_1 only has seven lines because much of the work is done by the DMX_1 and WWMA_1 subs.

The ADX is used in the calculation of the average directional movement rating ADR.

Other References

http://fxtrade.oanda.com/learn/graphs/indicators/adx.shtml#atr

http://www.marketvolume.com/technicalanalysis/adxr.asp

Like what you have just read? Digg it or Tip'd it.

Adaptive Price Zone

Adaptive Price Zone APZ

Read on for formula, calculation steps and VBA code. For naive backtest results and findings, visit here

The Adaptive Price Zone APZ indicator is from the Technical Analysis of Stocks & Commodities Magazine, September 2006 article "Trading With An Adpative Price Zone" by Lee Leibfarth. It has an upper and lower boundary and prices are expected to reverse when it hits either boundar.

Upper APZ boundary = EMA of (EMA of Price for n periods) for n periods + APZRange

Lower APZ boundary = EMA of (EMA of Price for n periods) for n periods – APZRange

where APZRange = EMA of (High – Low) for n periods x band factor.

Both band factor and n are the user’s choice. Band factor adjusts the width of the adaptive price zone. EMA refers to the exponential moving average. As can be seen, the adaptive price zone is based on the exponential moving average of an exponential moving average.

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate APZ. Method B is faster and more flexible.

Method A

Like the Chaikin oscillator, the adaptive price zone can be computed using a series of exponential moving average custom functions. Nonetheless, a custom function to compute the APZ is provided below. Note that it is an array function and outputs the center line, upper and lower bands of the adaptive price zone. To display the entire set of outputs, enter the APZ function into the one cell and select it along with the 2 cells horizontally next to it, press F2 and Enter.

Your inputs are both the current and last price and range EMAs, as well as the band factor and average period n. Your VBA code must include the EMA function for the APZ function to work.

'Paste this code into your ThisWorkBook code window in VBA. Right Click This WorkBook in Project Explorer and click View Code.

Private Sub Workbook_Open()

AddUDF

End Sub

'The rest belong to any module

Sub AddUDF()

'Tells Excel to includes these in list of functions, add descriptions to them and create a new category called Technical Indicators.

Application.MacroOptions macro:="APZ", _

Description:="Returns the center line, upper band and lower band the adaptive price zone" & Chr(10) & Chr(10) & _

"Input current EMA of price, last period's EMA of price, current EMA of (High-Low), last period's EMA of (High-Low), band_factor and n the averaging period.", _

Category:="Technical Indicators"

End Sub

Public Function APZ(CurrentEMA_Price, LastEMA_Price, CurrentEMA_Range, LastEMA_Range, band_factor, n)

Dim result(0, 1 To 3)

result(0, 1) = EMA(LastEMA_Price, CurrentEMA_Price, n)

bandwidth = EMA(LastEMA_Range, CurrentEMA_Price, n) * band_factor

result(0, 2) = result(0, 1) + bandwith

result(0, 3) = result(0, 1) - bandwidth

APZ = result

End Function

Once you are done with the above, you can calculate the adaptive price zone by entering into any cell, "=APZ(Current EMA of Price, Last EMA of Price, Current EMA of Range, Last EMA of Range, band factor, n)". As such, you need to calculate the respective EMAs before hand. Select the cell and its 2 neighbours, press F2 and Enter to display the entire set of outputs.

Method B

Method B offers the benefit of not having you calculation any exponential averages in advance. It does everything for you. To run Method B, you have to copy the Runthis sub and the EMA sub of Method B from the page on Accumulation/Distribution line and exponential moving average into your module. You will run the APZ sub from the Runthis sub.

'Copy the following line into the Runthis sub

'Just before the line End Sub

'Disable all other macros that Runthis will call e.g. CLV, ADL, by

'marking them out as comments with single quotes

Dim band_factor As Double

band_factor=2

'Range_1 high, low, output

APZ_1 high, low, close1, output, band_factor, n

Sub Range_1(high, low, output)

output(0, 1).Value = "Range"

high0 = high(1, 1).Address(False, False)

low0 = low(1, 1).Address(False, False)

output(1, 1).Value = "=" & high0 & "-" & low0

output(1, 1).Copy output

End Sub

Sub APZ_1(high As Range, low As Range, close1 As Range, output As Range, band_factor As Double, n As Long)

'Use the Range and EMA functions to calculate components of the APZ

EMA close1, output, n

output(0, 1).Value = "EMA_Price"

Range_1 high, low, output.Offset(0, 1)

EMA output.Offset(0, 1), output.Offset(0, 2), n

output(0, 3).Value = "EMA_Range"

output0 = output(1, 3).Address(False, False)

output(0, 4).Value = "APZ_Width"

output(1, 4).Value = "=" & output0 & "*" & band_factor

output(1, 4).Copy output.Offset(0, 3)

output(0, 5).Value = "APZ_Upper"

output0 = output(4, 6).Address(False, False)

output1 = output(4, 4).Address(False, False)

output(4, 5).Value = "=" & output0 & "+" & output1

output(0, 7).Value = "APZ_Lower"

output(4, 7).Value = "=" & output0 & "-" & output1

output(4, 5).Copy output.Offset(0, 4)

output(4, 7).Copy output.Offset(0, 6)

EMA output, output.Offset(0, 5), n

output(2, 6).Copy output(3, 6)

output(0, 6).Value = "APZ_Center"

Range(output(1, 5), output(2, 7)).Clear

End Sub

Other References

http://www.traders.com/documentation/FEEDbk_docs/2006/09/TradersTips/TradersTips.html#tradestation

Like what you have just read? Digg it or Tip'd it.

Sunday, June 28, 2009

Chaikin Oscillator

Chaikin Oscillator COSC

Comes with formula, calculation steps and VBA code

Introduction

The Chaikin oscillator is very similar to the Chaikin money flow, except that it is actually the difference between two moving averages of the Accumulation/Distribution line or ADL. Some articles uses a simple moving averge, while some propose that an exponential moving average be used instead. I choose the exponential moving average. The Chaikin oscillator is calculated as such:

Chaikin Oscillator=n period EMA of the ADL - k period EMA of the ADL

An n period exponential moving average has a decay factor of 2/(n+1). An article on the exponential moving average, its formula and VBA code can be found here, while the Accumulation/Distribution line and its VBA code is covered in an article here.

VBA Code

Method A uses functions, while Method B uses sub procedures to calculate CMF. Method B is faster and more flexible.

Method A

Insert the VBA code for Method A of the Accumulation/Distribution line.

Insert the VBA code for Method A of the exponential moving average.

Calculate ADL on another column in your spreadsheet either using your own formula or the ADL function provided by me. If you are using my custom functions, you just need to enter into any cell, "=ADL([Last period ADL],[Current High], [Current Low], [Current Close],[Current Volume])" to compute current ADL.

Compute a fast exponential moving average for the ADL. Using my custom function, you enter into any cell, "=EMA([Last Period EMA],[Current ADL],[n])". Enter last period ADL as last period EMA when you are computing the first EMA of your dataset. [n] is your averaging period. Repeat the above with a larger average period. The Chaikin oscillator is the difference between the slow moving average and the fast moving average

If you must have a custom function to work with, you can follow the instructions below. You will still need to insert the VBA code for the ADL and EMA functions. The COSC function is an array function that will output the Chaikin Oscillator, ADL, Fast EMA, Slow EMA.

'Paste this code into your ThisWorkBook code window in VBA. Right Click This WorkBook in Project Explorer and click View Code.

Private Sub Workbook_Open()

AddUDF

End Sub

'The rest belong to any module

Sub AddUDF()

'Tells Excel to includes these in list of functions, add descriptions to them and create a new category called Technical Indicators.

Application.MacroOptions macro:="COSC", _

Description:="Returns Chaikin Oscillaor, current ADL, Fast EMA and Slow EMA." & Chr(10) & Chr(10) & _

"Input current high, low, close, volume, n, k, last period's ADL,fast EMA and slow EMA. n and k are the averaging periods for the fast and slow moving averages respectively.", _

Category:="Technical Indicators"

End Sub

Public Function COSC(high, low, close_, volume, n, k, ADLYesterday, FastEMAYesterday, SLowEMAYesterday)

Dim result(0, 1 To 4)

result(0, 2) = ADLYesterday + CLV(high, low, close_) * volume 'ADL

result(0, 3) = EMA(FastEMAYesterday, result(0, 2), n) 'EMAFast

result(0, 4) = EMA(SLowEMAYesterday, result(0, 2), k) 'EMASlow

result(0, 1) = result(0, 3) - result(0, 4) 'Oscillator

COSC = result

End Function

Once you are done with the above, you can compute Chaikin oscillator by entering into any cell, "=COSC([Current High], [Current Low], [Current Close],[Current Volume],...)". Select the cell and the three cells horizontally next to it, press F2 and Enter to display the full set of outputs.

Method B

To run Method B, you have to copy the Runthis sub and the CLV, ADL and EMA sub of Method B from the page on Accumulation/Distribution line and exponential moving average into your module. You will runthe COSC sub from the Runthis sub.

'Copy the following line into the Runthis sub
'Just before the line End Sub
'Disable all other macros that Runthis will call e.g. CLV, ADL, by
'marking them out as comments with single quotes
COSC_1 high, low, close1, volume, output, n, k

Sub COSC_1(high As Range, low As Range, close1 As Range, volume As Range, output As Range, n As Long, k As Long)
output(0, 6).Value = "Chaikin Oscillator"
'Calculate the ADL and EMA needed
ADL_1 high, low, close1, volume, output
EMA_1 output.Offset(0, 2), output.Offset(0, 3), n
EMA_1 output.Offset(0, 2), output.Offset(0, 4), k
'Calculate Chaikin oscillator
output0 = output(2, 4).Address(False, False)
output1 = output(2, 5).Address(False, False)
output(2, 6).Value = "=" & output0 & "-" & output1
output(2, 6).Copy output.Offset(0, 5)
output(1, 6).Clear
End Sub

Other References
http://www.gannalyst.com/Gannalyst_Professional/Gannalyst_Indicators_ChaikinOscillator.shtml

Like what you have just read? Digg it or Tip'd it.

Tuesday, June 30, 2009

Monday, June 29, 2009

Sunday, June 28, 2009

Followers